Bangun Datar

Jenis bangun datar yang dipelajari di sekolah antara lain; segitiga, jajargenjang, persegi, persegi panjang, segilima, dan lingkaran. Berikut penjelasan lengkap, ciri, serta rumus luas dan kelilingnya.

1. Segitiga

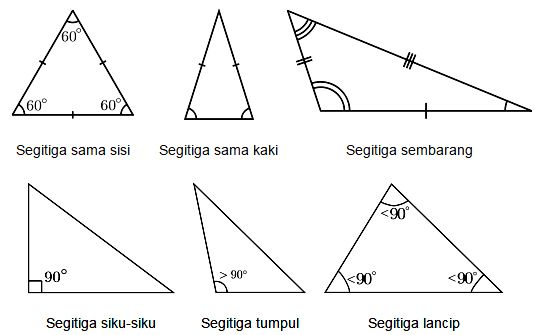
Segitiga adalah bangun datar yang memiliki tiga garis yang saling bertemu di ujungnya. Setiap ruas garis yang bertemu di ujung disebut sebagai sudut. Terdapat beberapa jenis segitiga, yaitu segitiga sama kaki, segitiga sama sisi, segitiga siku-siku, segitiga sembarang. Segitiga sama kaki adalah segitiga yang kedua sisinya sama panjang.

Segitiga sama sisi merupakan segitiga yang ketiga sisinya memiliki panjang yang sama. Lalu segitiga siku-siku adalah segitiga yang membentuk sudut siku-siku yaitu 90 derajat. Sedangkan segitiga sembarang adalah segitiga yang seluruh sisinya tidak sama panjangnya.

Rumus segitiga:

• Luas segitiga: 1/2 x alas x tinggi atau 1/2 x a x t
• Keliling segitiga: jumlah ketiga sisinya atau a + b + c

 

2. Jajargenjang

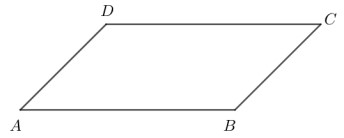
Jajar genjang adalah bentuk bangun datar yang memiliki empat sisi. Namun, berbeda dengan persegi dan persegi panjang, jajar genjang memiliki sepasang sisi yang sejajar. Terdapat jajar genjang memiliki bentuk lain, yaitu belah ketupat. Seperti namanya, belah ketupat mirip dengan bentuk ketupat.

Rumus jajargenjang:

• Luas jajar genjang: alas x tinggi atau a x t
• Keliling jajar genjang: 2 x (sisi sejajar 1 + sisi sejajar 2) atau 2(a + b)

 

3. Persegi Panjang

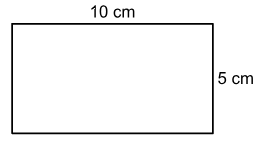
Persegi panjang adalah salah satu bentuk dari segi empat yang memiliki sisi yang panjang dan memiliki empat sudut siku-siku. Selain itu, persegi panjang memiliki dua sisi yang panjang, dan dua sisi lainnya yang pendek. Atau dengan kata lain, memiliki dua pasang sisi yang sama panjang dan sejajar.

Rumus persegi panjang:

• Luas persegi panjang: panjang x lebar atau p x l
• Keliling persegi panjang: 2 x (panjang + lebar) atau 2(p+l)

 

4. Persegi

Selain persegi panjang dan jajar genjang, persegi merupakan salah satu bentuk bangun datar dari segiempat juga. Berbeda dengan jajar genjang dan persegi panjang, persegi memiliki semua sisi yang sama panjang. Namun, seperti persegi panjang, persegi membentuk empat sudut siku-siku.

Rumus persegi:

• Luas persegi: sisi x sisi atau s²
• Keliling persegi: 4 x sisi atau 4s

 

5. Segi Lima

Sesuai namanya, segi lima merupakan bentuk bangun datar yang memiliki lima sisi. Nama lain dari segi lima adalah pentagon. Setiap sisi segi lima memiliki panjang yang sama dan beraturan. Selain itu, kelima sisi dari segi lima juga saling berhubungan dan setiap sudutnya membentuk 108 derajat.

Rumus segi lima:

• Luas segi lima: (diagonal 1 x diagonal 2 x sin(36°)) / 2
• Keliling segi lima: sisi 1 + sisi 2 + sisi 3 + sisi 4 + sisi 5

 

6. Lingkaran

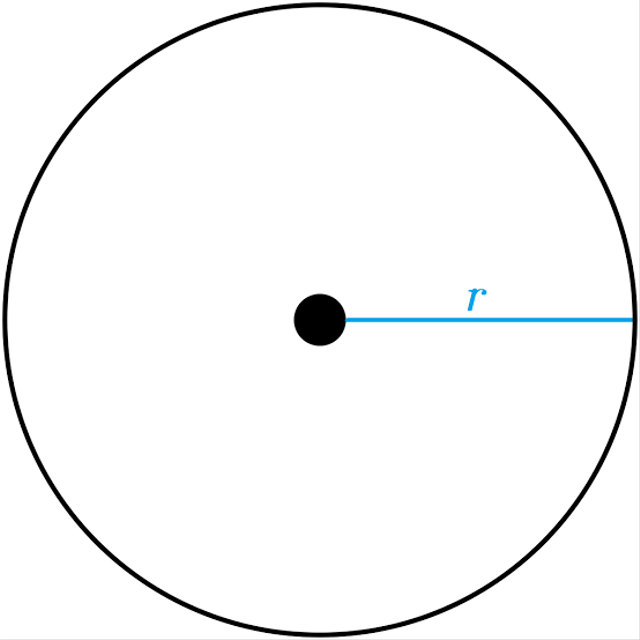
Berbeda dengan bangun datar lainnya, lingkaran adalah bentuk bangun datar yang tidak memiliki sisi, dan memiliki garis yang bundar, tidak membentuk sudut lancip atau sudut tumpul seperti bangun datar lainnya. Lingkaran merupakan bangun datar yang berpusat di titik pusat. Setiap titik ujung lingkaran memiliki panjang yang sama dari titik pusat lingkaran. Lingkaran juga memiliki sudut 180 derajat. Jarak dari titik pusat ke titik ujung lingkaran disebut dengan jari-jari.

Rumus lingkaran:

• Luas lingkaran: πr² atau phi kali jari-jari kuadrat
• Keliling lingkaran: 2πr atau 2 phi kali jari-jari

 

Pengertian Kekongruenan Dan Kesebangunan

Jika bicara tentang kongruen, maka tidak lepas dari pembahasan mengenai kesebangunan. Kekongruenan dan kesebangunan memang terlihat mirip, namun juga memiliki beberapa perbedaan. Untuk memahami dengan lebih baik, kamu bisa membaca penjelasan di bawah ini.

Pengertian Kongruen

Secara sederhana, bangun datar kongruen adalah istilah yang digunakan untuk menyatakan dua objek bangun datar yang sama persis. Baik secara ukuran, sudut, ataupun sifat. Sebagai contoh, dua buah segitiga baru bisa dikatakan kongruen jika memiliki sisi-sisi yang bersesuaian sama panjang dan sudut-sudut yang bersesuaian sama besar sehingga memiliki ukuran yang sama persis. 

Dalam matematika, tanda kongruen dilambangkan dengan simbol "≡" atau “≅" yang disebut “tanda sama dengan garis ganda”. Tanda ini artinya bahwa dua objek tersebut memiliki kesamaan yang sama persis.

Penerapan kongruen dalam kehidupan sehari-hari adalah saat membuat jendela atau pintu rumah. Lubang jendela harus kongruen dengan daun jendela. Sehingga, daun jendela dapat terpasang dengan tepat dan rapi.

Pengertian Kesebangunan

Kesebangunan adalah istilah yang digunakan bila dua objek tersebut memiliki proporsi yang mirip satu sama lain. Jika dua bangun memiliki bentuk yang sama dan ukuran yang berbeda-beda maka dapat dikatakan sebangun. 

Jika menggunakan contoh segitiga, maka segitiga yang sebangun memiliki sudut dengan besaran yang sama. Dan ketiga sisinya bersesuaian dengan perbandingan yang sama.

Dalam matematika, kesebangunan ditandai dengan simbol “≈” yang dibaca sebagai “sebangun dengan”. Tanda ini menunjukkan kalau dua objek tersebut merupakan objek yang sebangun.

Penerapan kesebangunan dalam kehidupan sehari-hari adalah saat pembuatan maket atau miniatur. Biasanya, miniatur dibuat dengan perbandingan skala yang lebih kecil. Misalnya maket 1:16 atau 1:100 dari ukuran aslinya.

Perbedaan Kekongruenan Dan Kesebangunan

Dari penjelasan sebelumnya tentang pengertian kekongruenan dan kesebangunan, kamu bisa menemukan adanya perbedaan antara dua istilah tersebut. Yaitu pada panjang sisi dua objek yang dibandingkan.

Dua buah objek atau bangun dapat dikatakan kongruen kalau sisi-sisi yang bersesuaian memiliki panjang yang sama. Sedangkan, objek atau bangun dikatakan sebangun jika sisi-sisi yang bersesuaian memiliki perbandingan yang sama besar.

Sehingga, dapat disimpulkan kalau dalam teori kekongruenan dan kesebangunan, setiap objek yang kongruen sudah pasti sebangun. Namun, objek yang sebangun belum tentu kongruen.

Syarat-syarat Kekongruenan

Untuk mengetahui apakah dua buah bangun kongruen sebenarnya sangat mudah. Kamu hanya perlu menumpuk dua bangun tersebut satu sama lain. Jika kedua bangun tersebut saling menutupi, maka benda tersebut dapat dikatakan kongruen.

Namun, secara formal, ada dua syarat yang harus dipenuhi agar objek atau bangun dapat dikatakan kongruen. Yaitu sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sama panjang. 

Agar lebih jelas, perhatikan gambar berikut ini:

1. Sudut-sudut yang bersesuaian sama besar

Kalau mengacu dari gambar di atas, segitiga PQR dan segitiga XYZ memiliki sudut-sudut yang bersesuaian sama besar. Yaitu ∠P = ∠X, ∠Q = ∠Y, dan ∠R = ∠Z. Artinya, syarat dua segitiga kongruen telah terpenuhi. Sehingga, segitiga PQR dapat dikatakan kongruen dengan segitiga XYZ.

2. Sisi-sisi yang bersesuaian sama panjang

Selanjutnya, sisi-sisi pada segitiga PQR dan XYZ juga memiliki panjang yang sama. Berikut sisi-sisi yang bersesuaian sama Panjang.

Sisi PQ = XY

sisi QR = YZ

sisi PR = XZ

Syarat-syarat Kesebangunan

Dalam konteks bangun datar, syarat kesebangunan bangun datar juga ada dua. Yaitu sudut-sudut yang bersesuaian harus sama besar dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama.

Agar lebih jelas, perhatikan gambar berikut ini: 

1. Sudut-sudut yang bersesuaian sama besar

Sama seperti syarat kongruen, dua objek yang sebangun harus memiliki sudut yang sama besar. Dalam gambar di atas, kamu bisa melihat kalau ∠A = ∠S, ∠B = ∠T, dan ∠C = ∠U. 

2. Sisi-sisi yang bersesuaian memiliki perbandingan yang sama

Selain itu, sisi yang bersesuaian harus memiliki perbandingan yang sama. Untuk mengetahuinya, kamu bisa menghitung perbandingan setiap sisi yang bersesuaian. Sebagai contoh:

• Sisi ST dan AB memiliki perbandingan yang sama atau dapat ditulis ST/AB = 3/6 = 1/2
• Sisi TU dan BC memiliki perbandingan yang sama atau dapat ditulis TU/BC = 3/6 = 1/2
• Sisi SU dan AC memiliki perbandingan yang sama atau dapat ditulis SU/AC = 3/6 = 1/2

Dari perhitungan tersebut diketahui kalau ST/AB = TU/BC = SU/AC . Ketiga pasang sisi-sisi yang bersesuaian pada gambar di atas memiliki perbandingan yang sama. Sehingga, segitiga ABC sebangun dengan segitiga STU. Namun, karena panjang sisinya berbeda, maka segitiga ABC tidak kongruen dengan segitiga STU.